Convex Optimization for Trajectory Generation: A Tutorial on Generating Dynamically Feasible Trajectories Reliably and Efficiently

[Paper] [Toolbox Documentation] [Code]

We review three important convex optimization-based trajectory generation methods: lossless convexification (LCvx), and two sequential convex programming (SCP) algorithms known as SCvx and GuSTO.

These methods were successfully applied to rocket landing, spacecraft hypersonic reentry, spacecraft rendezvous and docking, aerial motion planning for fixed-wing and quadrotor vehicles, and robot motion planning problems, and were succesfully deployed in high-profile rocket flights conducted by organizations like NASA, Masten Space Systems, SpaceX, and Blue Origin.

We open-source these SCP algorithms in a toolbox for fast nonlinear optimal control.

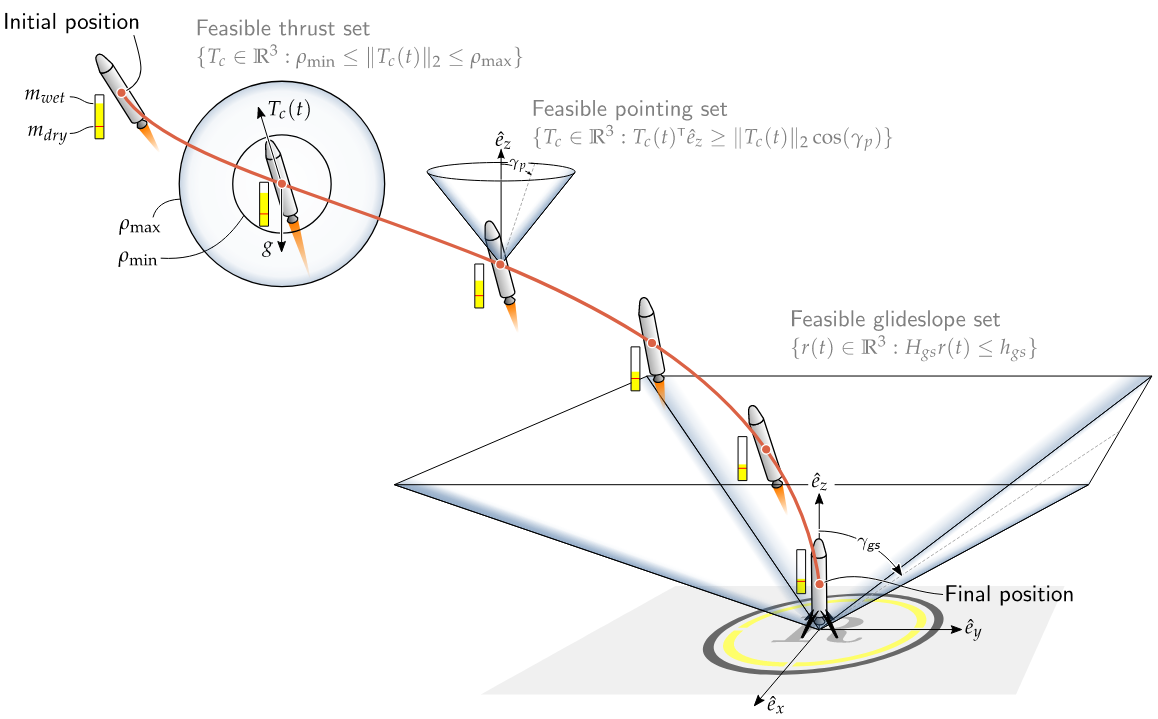
Abstract

Reliable and efficient trajectory generation methods are a fundamental need for autonomous dynamical systems of tomorrow. The goal of this article is to provide a comprehensive tutorial of three major convex optimization-based trajectory generation methods: lossless convexification (LCvx), and two sequential convex programming algorithms known as SCvx and GuSTO. In this article, trajectory generation is the computation of a dynamically feasible state and control signal that satisfies a set of constraints while optimizing key mission objectives. The trajectory generation problem is almost always nonconvex, which typically means that it is not readily amenable to efficient and reliable solution onboard an autonomous vehicle. The three algorithms that we discuss use problem reformulation and a systematic algorithmic strategy to nonetheless solve nonconvex trajectory generation tasks through the use of a convex optimizer. The theoretical guarantees and computational speed offered by convex optimization have made the algorithms popular in both research and industry circles. To date, the list of applications include rocket landing, spacecraft hypersonic reentry, spacecraft rendezvous and docking, aerial motion planning for fixed-wing and quadrotor vehicles, robot motion planning, and more. Among these applications are high-profile rocket flights conducted by organizations like NASA, Masten Space Systems, SpaceX, and Blue Origin. This article aims to give the reader the tools and understanding necessary to work with each algorithm, and to know what each method can and cannot do. A publicly available source code repository supports the numerical examples provided at the end of this article. By the end of the article, the reader should be ready to use each method, to extend them, and to contribute to their many exciting modern applications

Bibtex

@article{MalyutaEtAl2022,
author = {Malyuta, D. and Reynolds, T.~P. and Szmuk, M. and Lew, T. and Bonalli, R. and Pavone, M. and Acikmese, B.},
title = {Convex Optimization for Trajectory Generation},
year = {2022},
journal = {IEEE Control Systems Magazine},
volume = {42},
number = {5},
pages = {40--113}
}