I am a research scientist at the Toyota Research Institute, where I develop decision-making algorithms for autonomous systems. My research leverages tools from optimal and stochastic control, optimization, differential geometry, and machine learning, revealing insights for designing fast and reliable methods with optimality, accuracy, and adaptation guarantees. It was deployed on cars, drones, spacecraft and Mars rover testbeds, rockets, and mobile robotic manipulators.

Previously, I received my PhD from Stanford University advised by Marco Pavone and Riccardo Bonalli, completed research internships at Google Brain and NASA JPL, and studied at ETH Zurich and EPFL.

My Research

Some problems I have been working on:

• Optimization and control under uncertainty: How can we compute optimal trajectories for nonlinear systems that explicitly reason over uncertainty? Can we find low-dimensional structure in solutions and leverage GPU acceleration to efficiently solve these problems?
• Forward reachability analysis: How can we propagate uncertainty through complex systems (potentially with neural networks in the loop) in milliseconds and use it for planning and control? What accuracy can we expect? What problem structure can we exploit?
• Reliable and efficient learning-based control: How can a system (meta-)learn its dynamics, while handling the exploration-exploitation tradeoff and always satisfying constraints? How can we learn as fast as possible to enable reliable control of unstable systems?
• Resilient navigation: How can a drone autonomously fly even if all its exteroceptive sensors have failed?
• Vision-based control: How can a robot achieve precise control from high-dimensional visual inputs while ensuring safe and zero-shot deployment?

Preprints

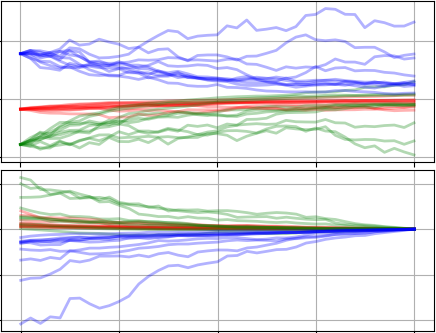Rough Stochastic Pontryagin Maximum Principle and an Indirect Shooting Method - T. Lew - Under Review - 2025
Project Page / Paper - We derive new optimality conditions and an indirect method for stochastic optimal control.

First, Learn What You Don’t Know: Active Information Gathering for Driving at the Limits of Handling - A. Davydov, F. Djeumou, M. Greiff, M. Suminaka, M. Thompson, J. Subosits, T. Lew - Under Review - 2024
Project Page / Paper - Unstable systems are difficult to simultaneously learn and control.

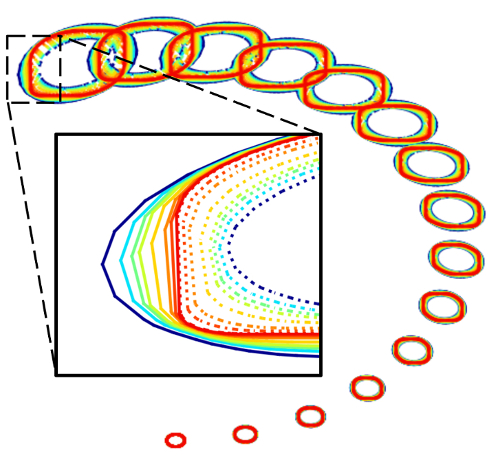Convex Hulls of Reachable Sets - T. Lew, R. Bonalli, M. Pavone - Under Review - 2024
Project Page / Paper / Code - We study the structure of convex hulls of reachable sets of nonlinear systems (dx/dt=f(x)+g(x)w).

Publications

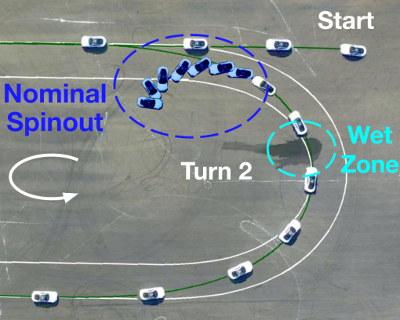Risk-Averse Model Predictive Control for Racing in Adverse Conditions - T. Lew, M. Greiff, F. Djeumou, M. Suminaka, M. Thompson, J. Subosits, - ICRA - 2025
Project Page / Paper - A risk-averse controller that can reason over uncertainty.

One Model to Drift Them All: Physics-Informed Conditional Diffusion Model for Driving at the Limits - F. Djeumou, T. Lew, N. Ding, M. Thompson, M. Suminaka, M. Greiff, J. Subosits - CoRL - Outstanding Paper Award - 2024
Project Page / Paper - A multimodal diffusion-based vehicle model for MPC.

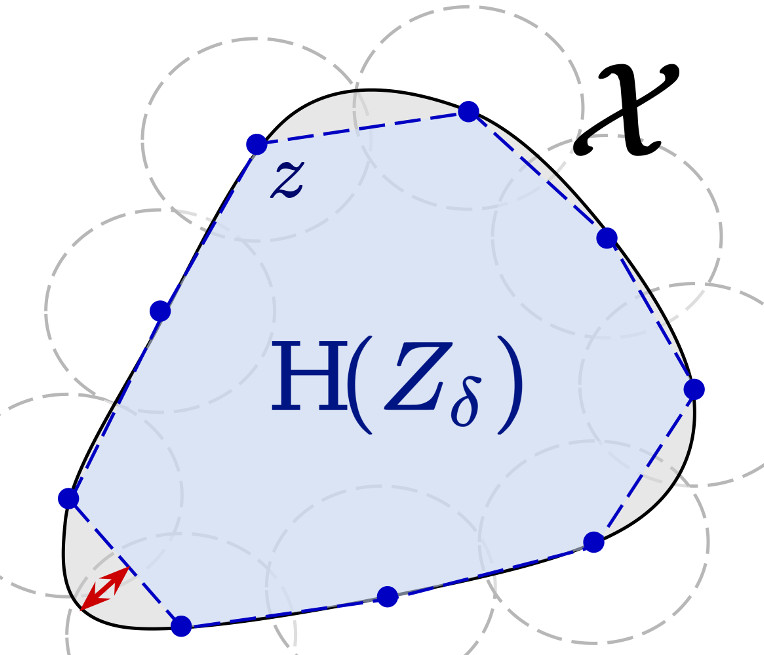Estimating the Convex Hull of the Image of a Set with Smooth Boundary: Error Bounds and Applications - T. Lew, R. Bonalli, L. Janson, M. Pavone - DCG - 2024
Project Page / Paper / Code - We study the problem of estimating the convex hull of the image of a compact set with smooth boundary.

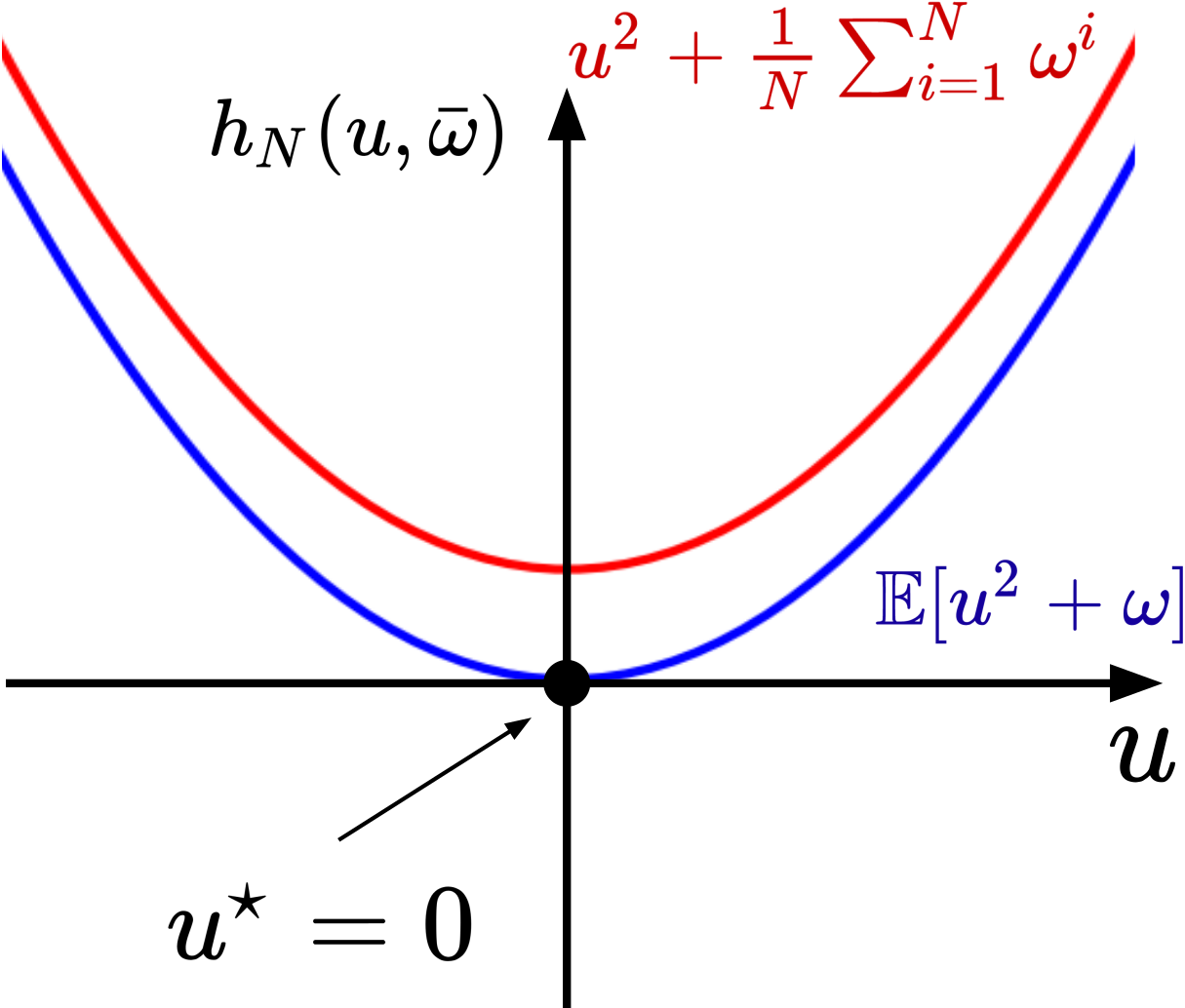Sample Average Approximation for Stochastic Programming with Equality Constraints - T. Lew, R. Bonalli, M. Pavone - SIOPT - 2024
Project Page / Paper / Code - We revisit the sample average approximation (SAA) approach for general non-convex stochastic programming and apply the method to stochastic optimal control problems.

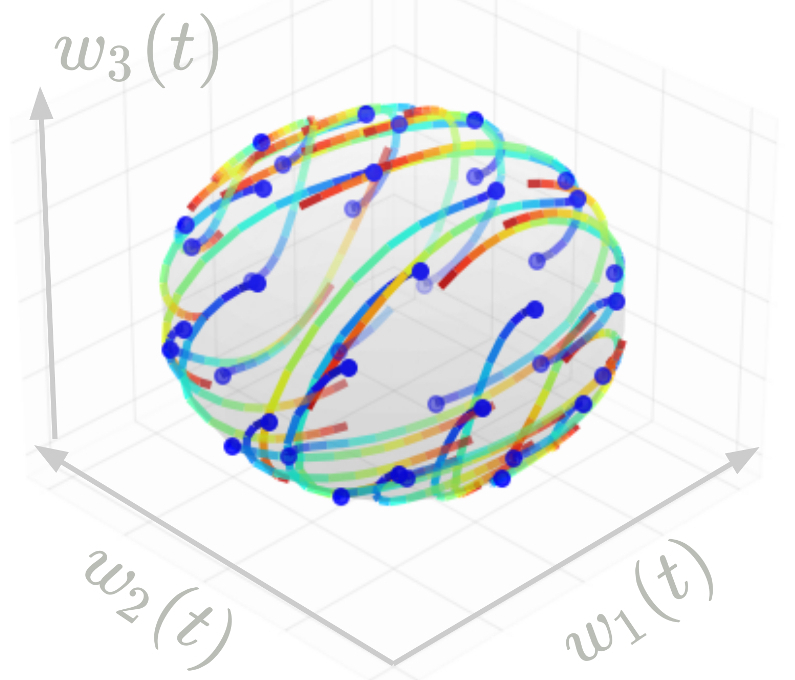Exact Characterization of the Convex Hulls of Reachable Sets - T. Lew, R. Bonalli, M. Pavone - CDC - Outstanding Student Paper Award - 2023
Project Page / Paper / Presentation / Code - We give a finite-dimensional characterization of the convex hulls of reachable sets of nonlinear systems (dx/dt=f(x)+w).

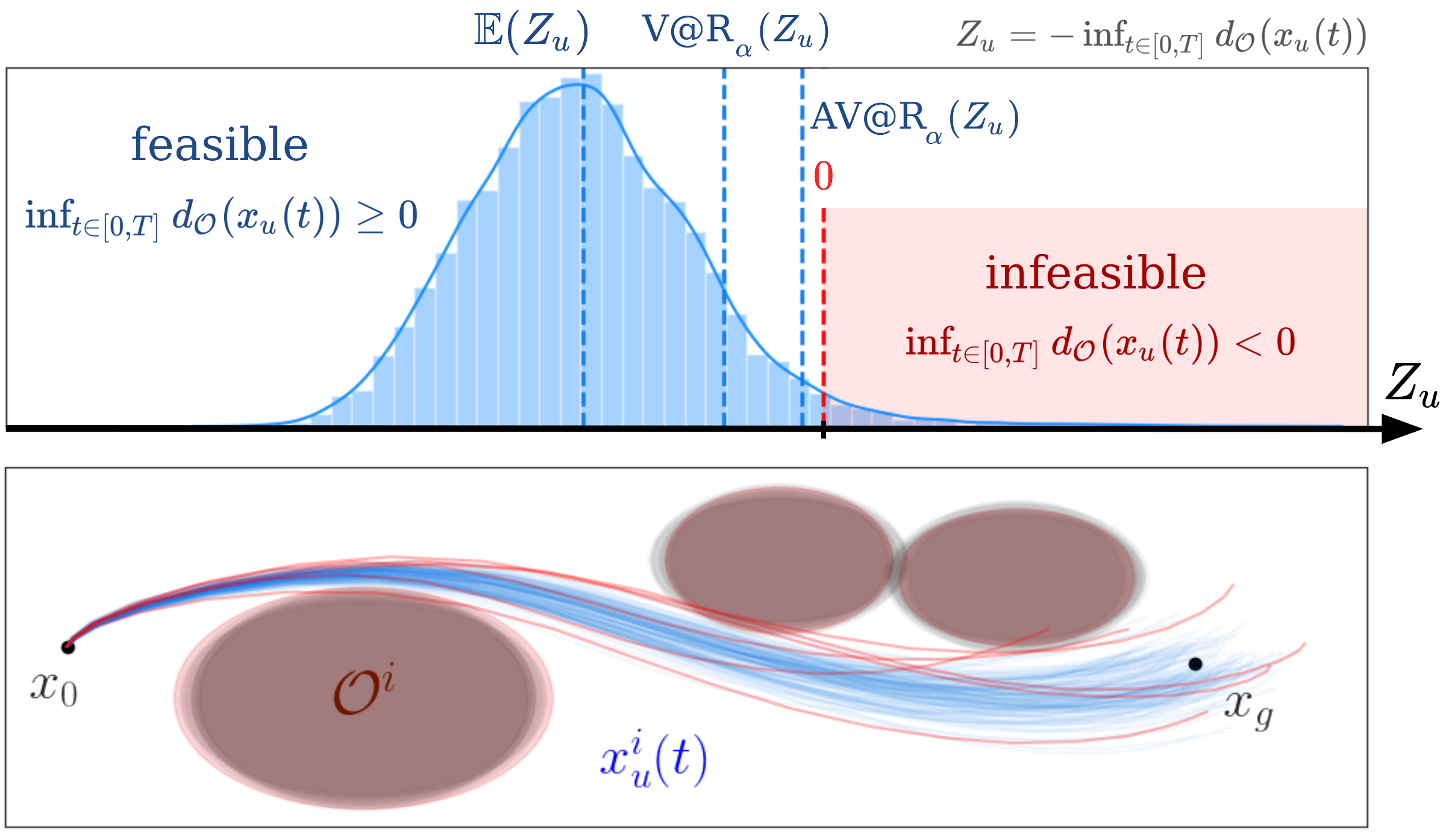Risk-Averse Trajectory Optimization via Sample Average Approximation - T. Lew, R. Bonalli, M. Pavone - RA-L - 2023
Project Page / Paper / Code - A sample-based approach to risk-averse trajectory optimization.

Robotic Table Wiping via Reinforcement Learning and Whole-body Trajectory Optimization - T. Lew, S. Singh, M. Prats, J. Bingham, J. Weisz, B. Holson, X. Zhang, V. Sindhwani, Y. Lu, F. Xia, P. Xu, T. Zhang, J. Tan, M. Gonzalez - ICRA - 2023
Project Page / Paper / Blog Post / Video - We propose an effective strategy for table wiping combining the strengths of reinforcement learning and whole-body trajectory optimization.

Sequential convex programming for non-linear stochastic optimal control - R. Bonalli, T. Lew, M. Pavone - ESAIM: COCV - 2022
Project Page / Paper / Code - We propose a sequential convex programming framework for non-linear finite-dimensional stochastic optimal control.

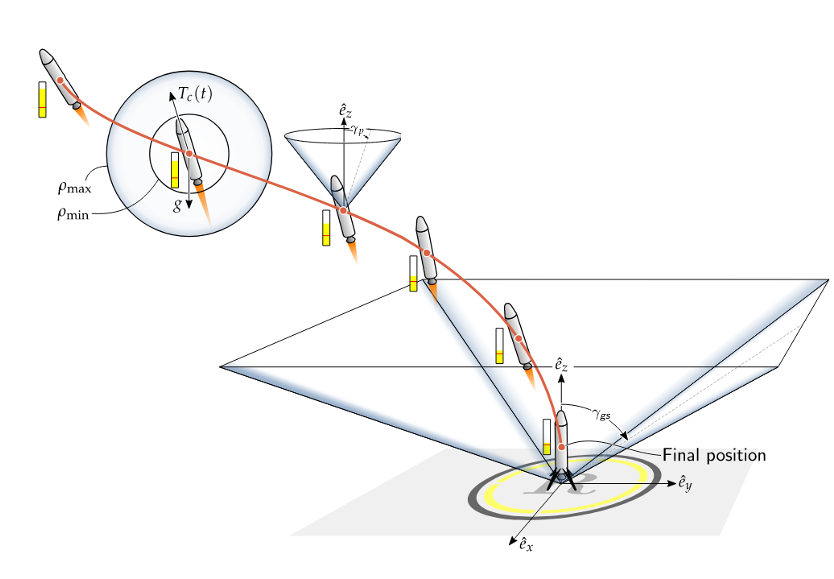Convex Optimization for Trajectory Generation: A Tutorial on Generating Dynamically Feasible Trajectories Reliably and Efficiently - D. Malyuta, T. Reynolds, M. Szmuk, T. Lew, R. Bonalli, M. Pavone, B. Açıkmeşe - CSM - Outstanding Paper Award - 2022
Project Page / Paper / Code - A comprehensive tutorial on convex trajectory optimization.

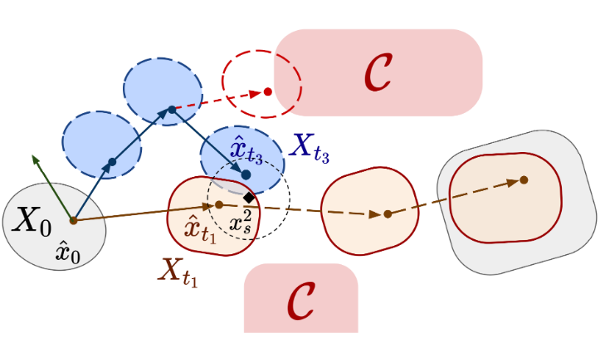Robust-RRT: Probabilistically-Complete Motion Planning for Uncertain Nonlinear Systems - A. Wu, T. Lew, K. Solovey, E. Schmerling, M. Pavone - ISRR - 2022
Project Page / Paper / Code - A robust sampling-based motion planning algorithm.

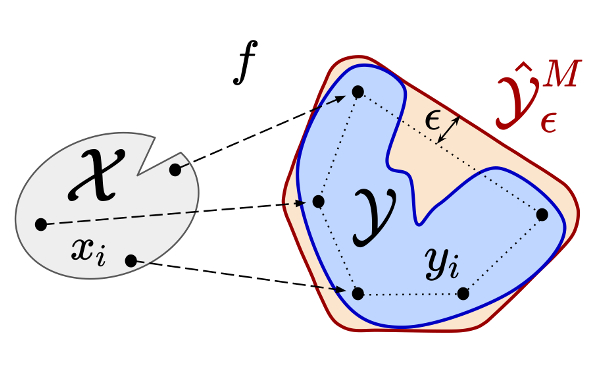A Simple and Efficient Sampling-based Algorithm for General Reachability Analysis - T. Lew, L. Janson, R. Bonalli, M. Pavone - L4DC - 2022
Project Page / Paper / Code / Video - We analyze a sampling-based reachability analysis algorithm.

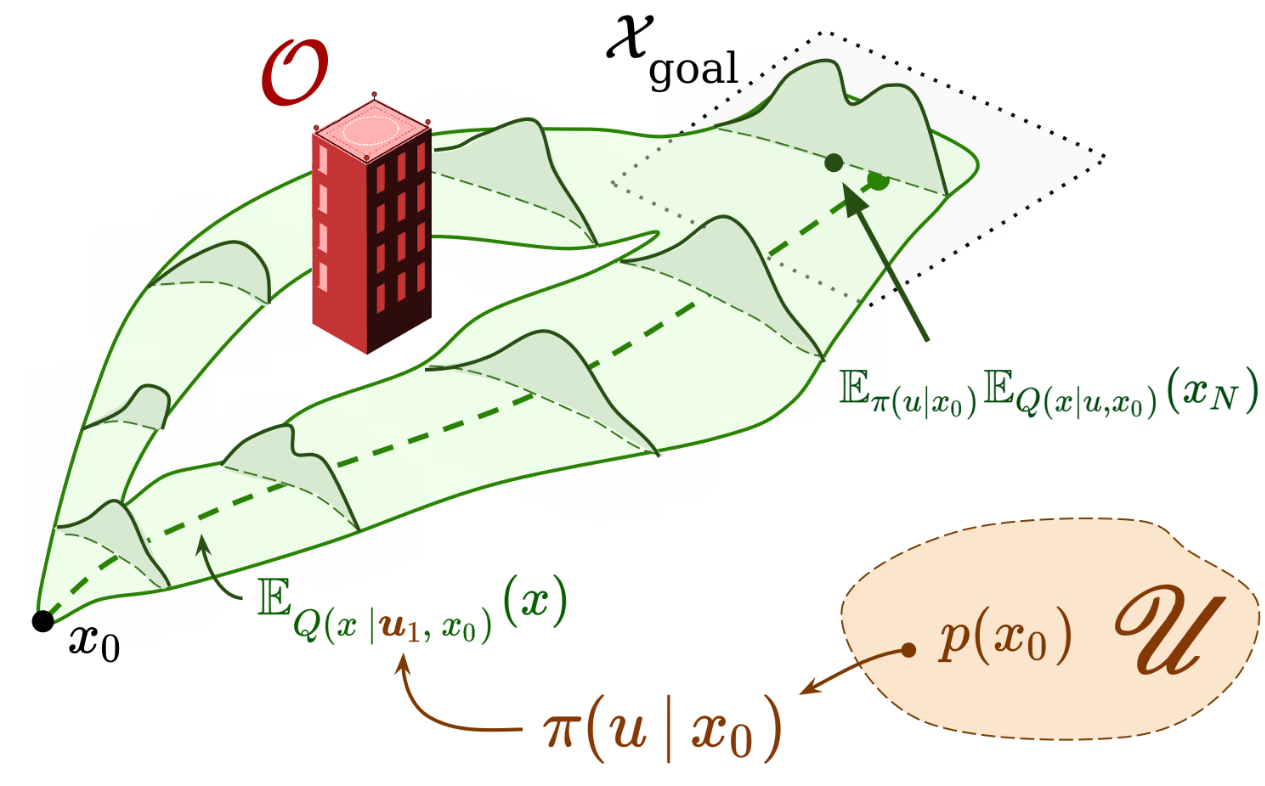Data-Driven Chance Constrained Control using Kernel Distribution Embeddings - A. J. Thorpe*, T. Lew*, M. M. K. Oishi, M. Pavone - L4DC - 2022
Project Page / Paper / Code - We present a data-driven algorithm for efficiently computing stochastic control policies for general joint chance constrained optimal control problems.

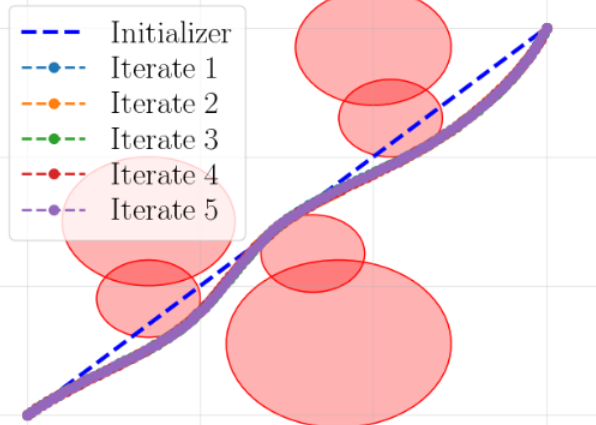Analysis of theoretical and numerical properties of sequential convex programming for continuous-time optimal control - R. Bonalli, T. Lew, M. Pavone - TAC - 2022
Project Page / Paper / Code - We analyze general SCP procedures for continuous-time optimal control.

Safe Active Dynamics Learning and Control: A Sequential Exploration-Exploitation Framework - T. Lew, A. Sharma, J. Harrison, A. Bylard, M. Pavone - T-RO - 2022
Project Page / Paper / Video / More Hardware Results - How can robots safely learn their dynamics?

Nebula: Quest for robotic autonomy in challenging environments; team costar at the darpa subterranean challenge - A. Agha-mohammadi et al - JFR - 2022
Project Page / Paper / CoSTAR-NeBula website - We present the algorithms, hardware, and software architecture deployed by the team CoSTAR in the DARPA SubT Challenge.

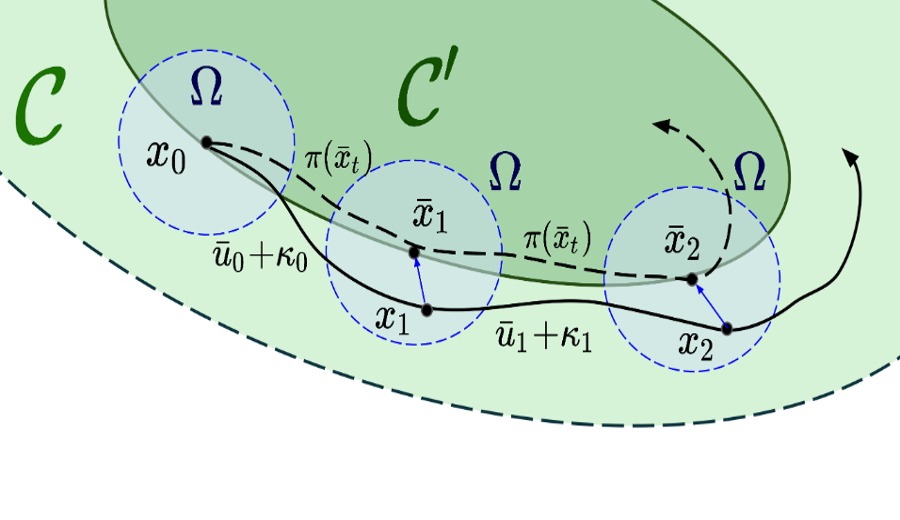Control Barrier Functions for Cyber-Physical Systems and Applications to NMPC - J. Schilliger, T. Lew, S. Richards, S. Hänggi, M. Pavone, C. Onder - RA-L - 2021
Project Page / Paper - We propose a CBF formulation that accounts for delays.

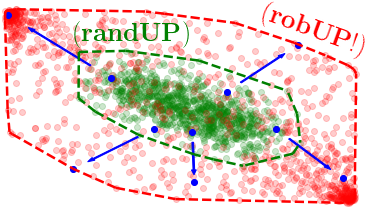Sampling-based Reachability Analysis: A Random Set Theory Approach with Adversarial Sampling - T. Lew, M. Pavone - CoRL - 2020
Project Page / Paper / Video / Code - New efficient sampling-based reachability analysis algorithms.

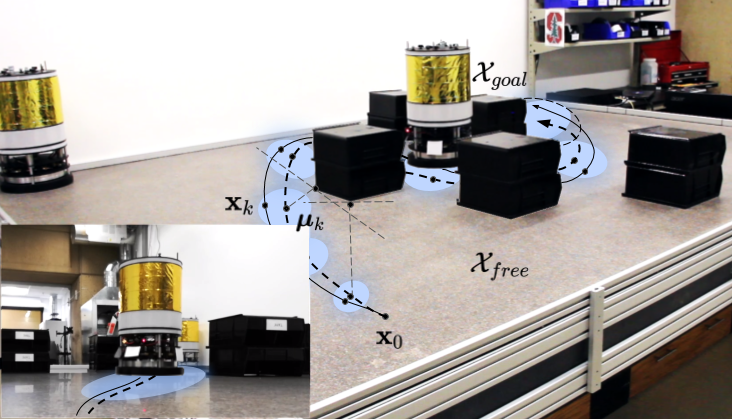Chance-Constrained Sequential Convex Programming for Robust Trajectory Optimization - T. Lew, R. Bonalli, M. Pavone - ECC - 2020
Project Page / Paper / Code - We propose an algorithm for chance-constrained trajectory optimization.

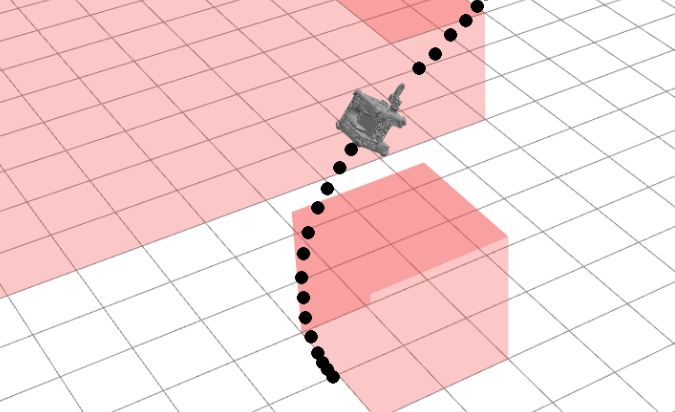Learning-based warm-starting for fast sequential convex programming and trajectory optimization - S. Banerjee, T. Lew, R. Bonalli, A. Alfaadhel, I. Alomar, H. Shageer, M. Pavone - AeroConf - 2020
Project Page / Paper / Code - A learning-based strategy to warm-start trajectory optimization tools.

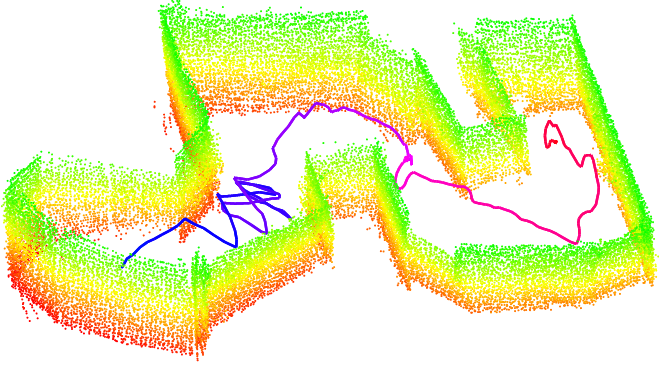Contact Inertial Odometry: Collisions are your Friends - T. Lew*, T. Emmei*, D. Fan, T. Bartlett, A. Santamaria-Navarro, R. Thakker, A. Agha-mohammadi - ISRR - 2019
Project Page / Paper / Video - How can a drone fly blindly, when all its exteroceptive sensors have failed?

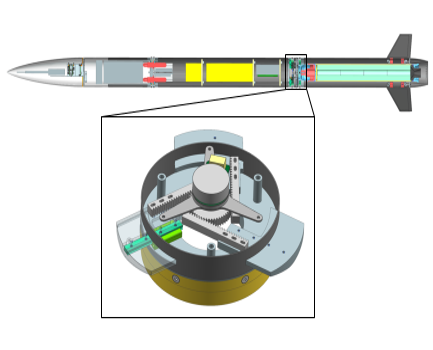Chance-Constrained Optimal Altitude Control of a Rocket - T. Lew, F. Lyck, G. Müller - EUCASS - 2nd Best Student Paper Award in Flight Dynamics, GNC and Avionics - 2019
Project Page / Paper / Launch Video / ARIS website - We propose a control algorithm for a rocket to accurately reach a target apogee.

Investigation of specific wheel-terrain interaction aspects using an advanced single wheel test facility - P. Oettershagen, T. Lew, A. Tardy, S. Michaud - ASTRA - 2019
Project Page / Paper - We identify limitations of wheel-soil interaction models and present a new method.

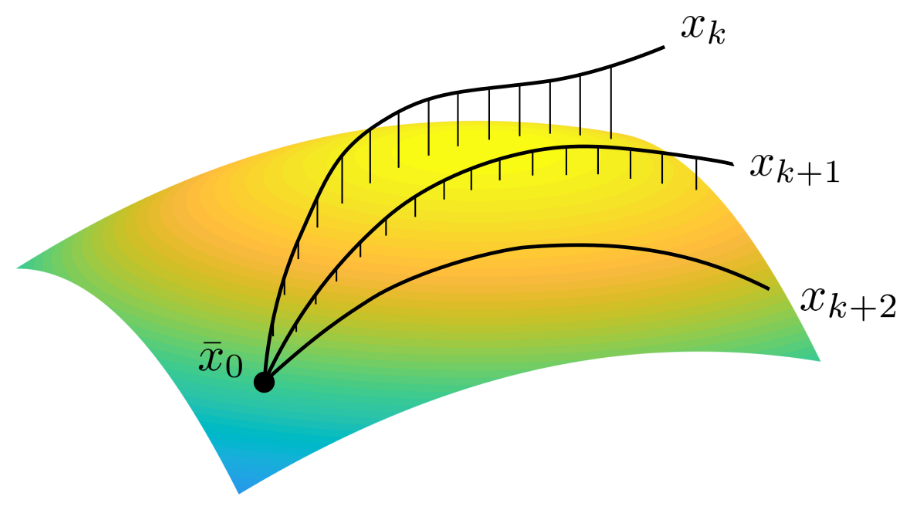Trajectory optimization on manifolds: A theoretically-guaranteed embedded sequential convex programming approach - R. Bonalli, A. Bylard, A. Cauligi, T. Lew, M. Pavone - RSS - 2019
Project Page / Paper / Code - A new SCP trajectory optimization algorithm on manifolds.