Estimating the Convex Hull of the Image of a Set with Smooth Boundary: Error Bounds and Applications

[Paper] [Code]

Abtract

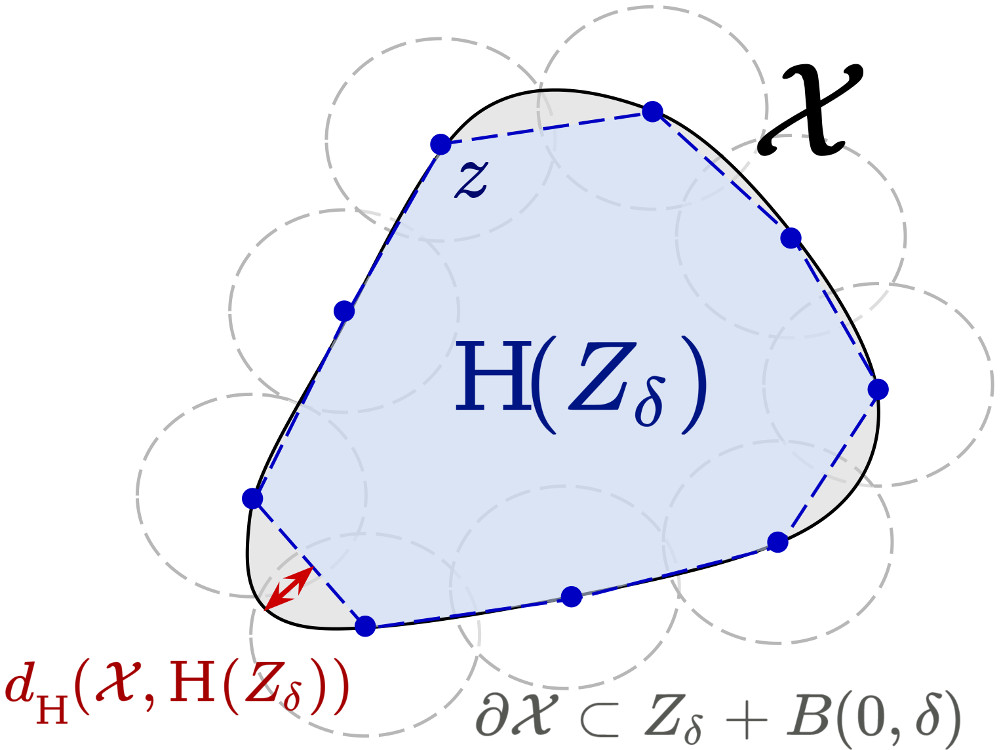
We study the problem of estimating the convex hull of the image f(X) of a compact set X with smooth boundary through a smooth function f. Assuming that the function is a diffeomorphism or a submersion, we derive new bounds on the Hausdorff distance between the convex hull of f(X) and the convex hull of the images f(xi) of M samples xi on the boundary of X. When applied to the problem of geometric inference from random samples, our results give tighter and more general error bounds than the state of the art. We present applications to the problems of robust optimization, of reachability analysis of dynamical systems, and of robust trajectory optimization under bounded uncertainty.

Connection to forward reachability analysis

The results in this paper better explain the accuracy of the sampling-based reachability analysis algorithm described in this project. In particular, we derive new error bounds that are significantly tighter than the bounds from this previous project. The missing piece was accounting for the smoothness of the boundaries of the sets of interest, which can be made rigorous using differential geometry and allows deriving tight error bounds for convex hull estimators.