Sampling-based Reachability Analysis: A Random Set Theory Approach with Adversarial Sampling

[Paper] [Video] [Code]

Reachability analysis is at the core of many applications. Generally, it entails characterizing the set of reachable states for a system at any given time in the future. For instance, planning a trajectory for a quadrotor carrying a payload of uncertain mass in severe wind requires ensuring that no reachable state collides with obstacles. In formal verification of neural networks, reachability analysis can be used to quantify the change in output for various input perturbations, and hence ensure prediction accuracy despite adversarial examples.

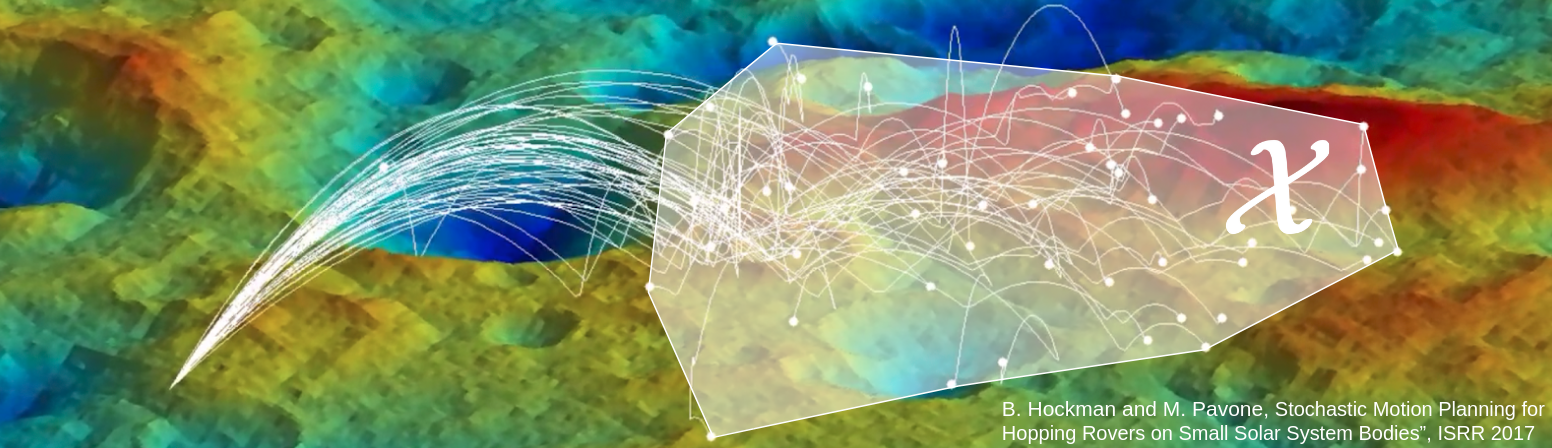
However, reachability analysis is notoriously challenging. In contrast to approaches which can handle problems with known probability distributions over parameters, sometimes only bounds on unknown parameters are available, which is the case when constructing confidence sets for the parameters of the model. To perform reachability analysis for problems with bounded uncertainty, current methods tend to be encumbered by strong assumptions, do not scale well to complex systems, or are too slow to be used within data-driven controllers which use and refine bounds on model parameters in real time. In practice, they often require tuning parameters used to provide theoretical guarantees or using a simplified model of the system. These are reasonable assumptions for many applications, but the general problem remains a challenge.

In this work, we propose a simple yet effective three-steps sampling-based reachability analysis algorithm for general nonlinear systems and bounded uncertainty:

1. initial states, controls, disturbances and parameters are sampled,
2. each particle is propagated according to the nonlinear dynamics,
3. the convex hull at each time is computed.

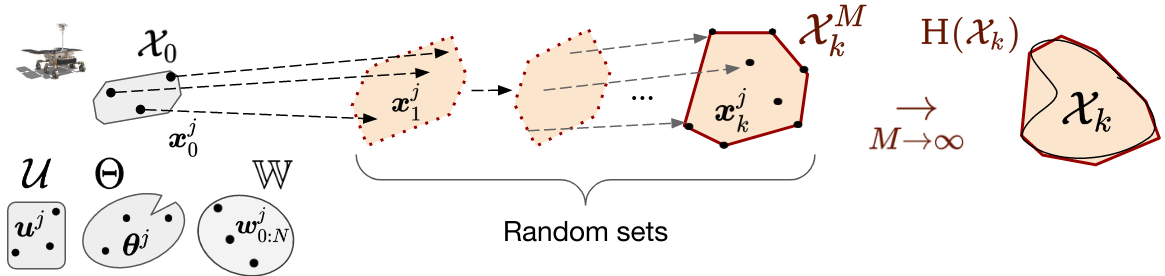
Using the theory of random sets, we prove that our method asymptotically converges to the convex hull of the reachable sets.

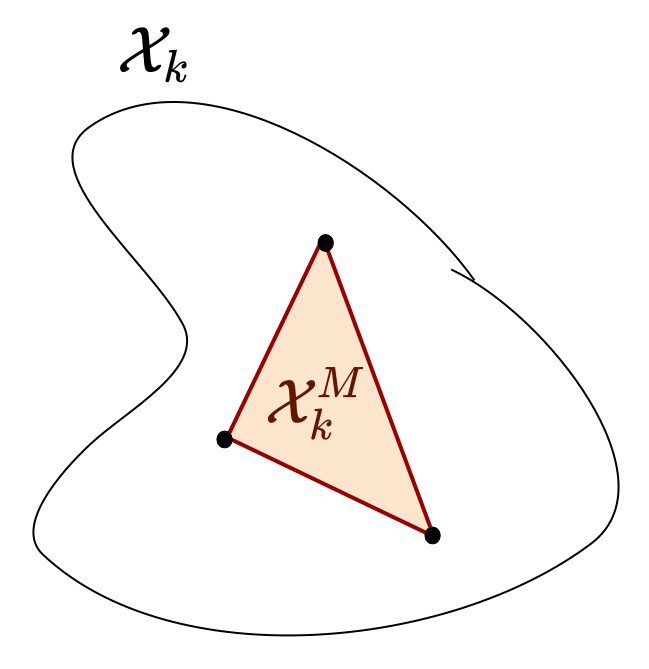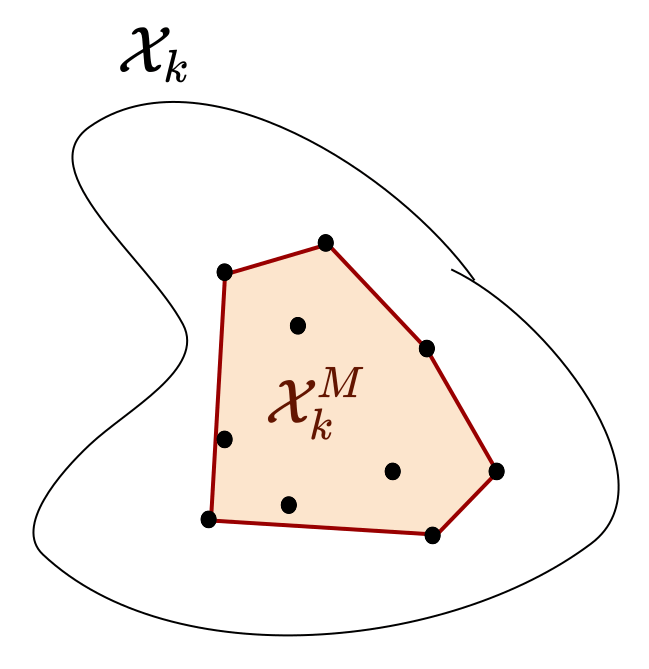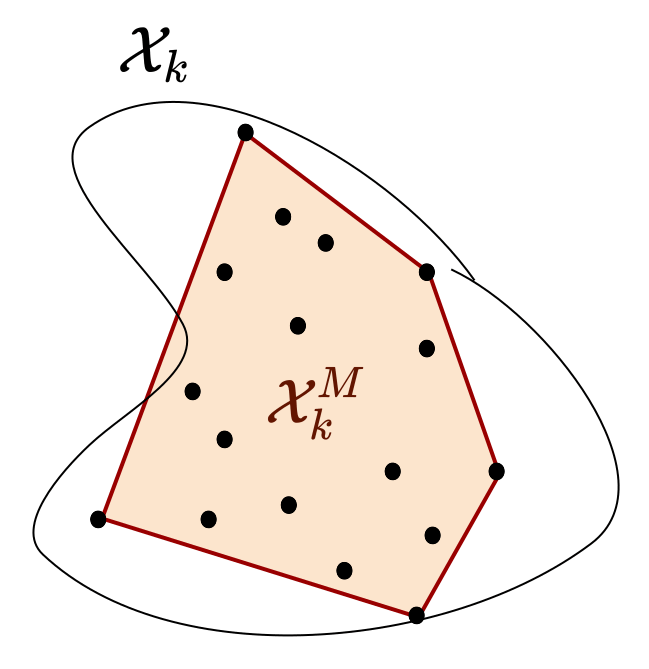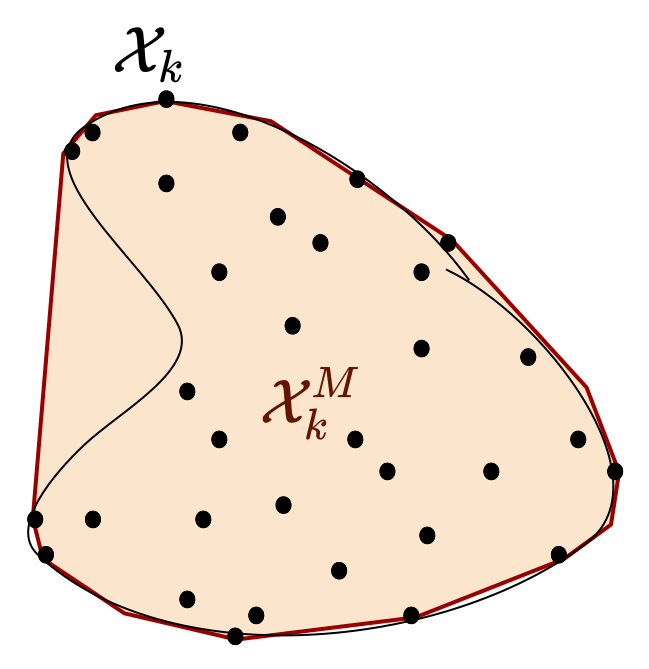
But how can we best select the samples for both efficiency and accuracy? We propose a new adversarial sampling approach to robustify our algorithm and accelerate its convergence. Intuitively, it pushes the image of the samples so they lie on the boundary of the true reachable set.

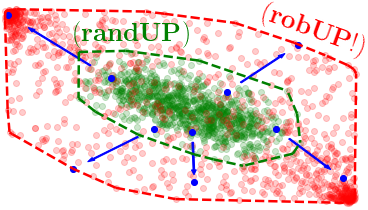
We show that our method out-performs previous approaches, demonstrate it on a system with learned neural-network dynamics, and use it to compute robust trajectories for a 13D nonlinear spacecraft system.

In later works, we use the algorithm for robust motion planning, safe active dynamics (meta-)learning, and derive finite-sample error bounds to quantify the accuracy of the method.

Bibtex

@inproceedings{randup_2020,
	title={Sampling-based Reachability Analysis: A Random Set Theory Approach with Adversarial Sampling},
	author={Lew, T. and Pavone, M.},
	booktitle={Conference on Robot Learning},
	year = {2020},
}