Exact Characterization of the Convex Hulls of Reachable Sets

[Paper] [Presentation] [Code]

We study the convex hulls of reachable sets of nonlinear systems with bounded disturbances (dx/dt=f(x)+w). Reachable sets play a critical role in control, but remain notoriously challenging to compute. Is there additional problem structure that we can use to design faster and more accurate algorithms?

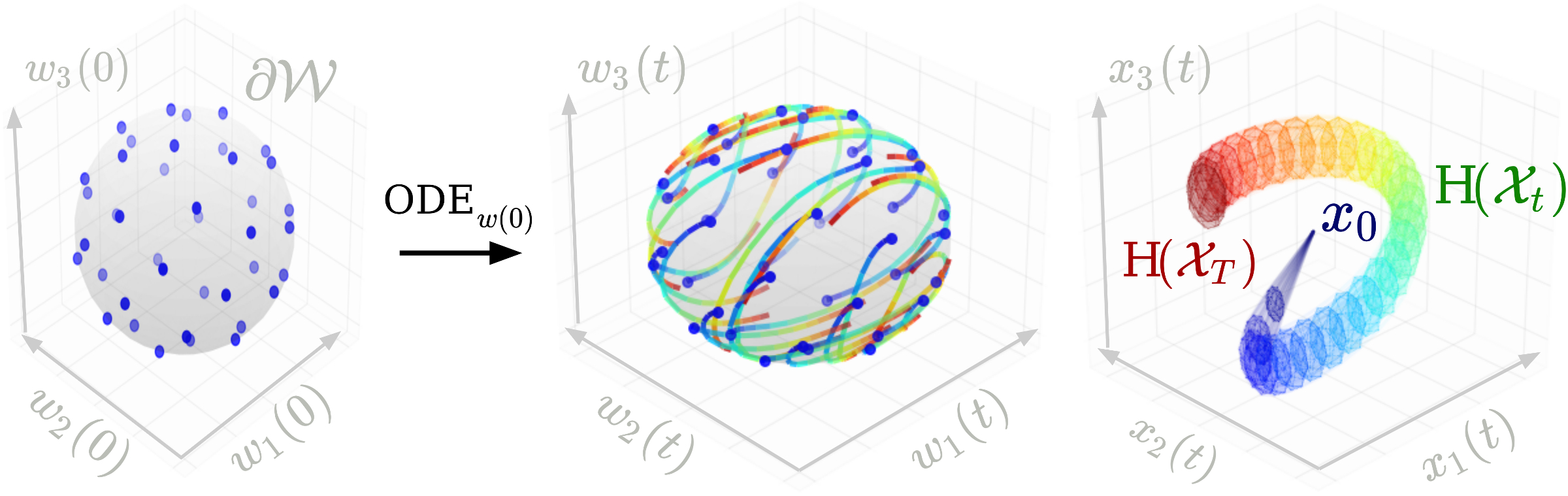
In this work, we exactly characterize the convex hulls of reachable sets as the convex hulls of solutions of an ordinary differential equation from all possible initial values of the disturbances. This finite-dimensional characterization unlocks an accurate and fast estimation algorithm to over-approximate reachable sets. We present applications to neural feedback loop analysis and robust model predictive control.